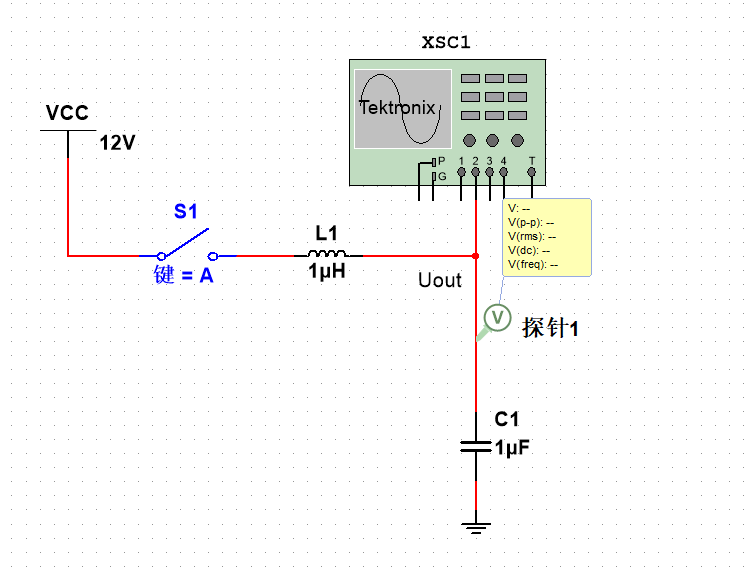
分析上图开关闭合后U_out随时间的变化，步骤如下：

电容：$I=C\frac{{\rm d}U}{{\rm d}t}$
电感：$U=L\frac{{\rm d}I}{{\rm d}t}$

列电路的电压关系

$$U_{out}+U_L=U_{VCC}$$

带入电感公式，得

$$U_{out}+L\frac{{\rm d}I}{{\rm d}t}=U_{VCC}$$

带入电容公式，得

$$U_{out}+LC\frac{{\rm d}^2 U_{out}}{{\rm d}t^2}=U_{VCC}$$

这是一个二阶常系数非齐次线性微分方程，解为齐次通解+非齐次特解，懒得写具体解法了，就是代公式。

齐次通解为

$$u^{'}(t)=C_1\cos{\frac{t}{\sqrt{LC}}}+C_2\sin{\frac{t}{\sqrt{LC}}}$$

特解是一个常数。把$U_{out}=C_0$带入原方程，解得$C_0=U_{VCC}$。

此时解为

$$u(t)=C_1\cos{\frac{t}{\sqrt{LC}}}+C_2\sin{\frac{t}{\sqrt{LC}}}+U_{VCC}$$

找初始条件。注意到$t=0$时，$U_{out}=0$，$I=0$，结合电容公式，$\frac{{\rm d}U_{out}}{{\rm d}t}=0$，解得$C_1=-U_{VCC}$，$C_2=0$，所以

$$U_{out}=-U_{VCC}\cos{\frac{t}{\sqrt{LC}}}+U_{VCC}$$

令L=1H，C=1F，仿真一下

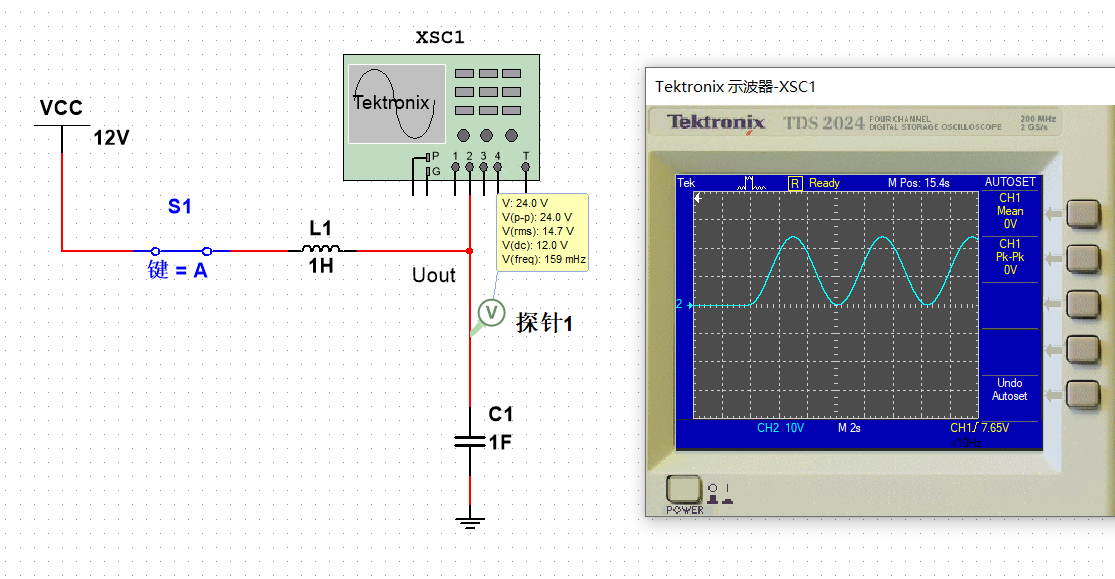
结果正确。

---

附一个表，输入LC参数自动计算频率。

L(H)	C(F)	ω(rad/s)	T(s)	f(Hz)
1	1	1	6.28	0.16

Q.E.D.